Лазерные сканеры калибруются производителями непосредственно после производства. После поставки лазерного сканера заказчику может быть произведена калибровка системы на основе калибровочного полигона. Кроме того, производители предлагают калибровку также в качестве услуги. Процесс заводской калибровки считается важным вопросом для большинства производителей, и поэтому объем раскрываемой информации значительно отличается, в зависимости от конкретного изготовителя.
Так, например, перед калибровкой каждый сканер Leica серии P или C доводится до так называемого нейтрального состояния сборки, подвергая его воздействию диапазон температур в течение нескольких дней в специальных камерах [11]. Кроме того, в течение этого периода каждый сканер работает в пределах рабочего диапазона. Этот шаг предназначен для снятия напряжений, накопленных во время сборки инструмента. Поскольку компоненты сканера изготовлены из различных материалов с различными коэффициентами теплового расширения, температурные колебания приводят к небольшим изменениям абсолютного и относительного положения компонентов, направляющих лазерный луч. Таким образом, угловая калибровка выполняется по всему диапазону условий окружающей среды в соответствии со спецификациями сканера. Это достигается путем установки сканера в специальной камере с окнами в определенных местах. Leica использует пары коллимированных телескопов, направленных друг на друга и размещенных вне камеры, чтобы обнаружить лазерный луч. Эти телескопы могут наблюдать друг за другом, когда сканер не помещен между ними так, чтобы относительная ориентация осей этих телескопов была известна с высокой точностью.
Для калибровки лазерный сканер помещается на коллимированную ось телескопической пары. Зная номинальное относительное положение коллимированных телескопов и лазерного сканера, фактическое угловое положение лазерного луча, направленного в один из телескопов, могут быть получены путем обработки изображений с помощью датчика, размещенного в фокальной плоскости телескопов. Измерение углового положения лазерного луча в двух гранях сканера по крайней мере для четырех направлений позволяет оценить угловые калибровочные параметры в модифицированном пучке регулировки. Параметры включают: смещение по азимуту, смещение по высоте, смещение зеркала и смещение лазера. Эти параметры и их зависимость от температуры хранятся в памяти прибора. Чтобы применить поправки, фактическая температура прибора измеряется во время сканирования в различных местах по всей внутренней части прибора. Действительность параметров ограничена во времени, и калибровку необходимо повторять через определенные производителем промежутки времени.
Коррекция наклона неразрывно связана с угловыми измерениями. Поэтому калибровка соответствующих датчиков также актуальна. Опять же, её необходимо проводить в экологической камере, чтобы смоделировать зависимость от условий окружающей среды. Камера включает в себя наклонный стол и эталонный датчик наклона для этой цели. Кроме того, для этого используется отдельный калибровочный стенд, а сама калибровка происходит при комнатной температуре. На этом стенде лазерный луч сканера направлен на эталонный блок, оснащенный камерой, способной воспринимать лазерный луч. Наклонный стол, на котором установлен сканер, может выполнять различные движения. Связывая выходной сигнал датчика наклона сканера с выходным сигналом опорного датчика, можно получить параметры регулировки наклона, такие как смещение и масштаб [11].
Калибровка блока измерения расстояния направлена на определение аддитивной постоянной и масштабного коэффициента. Как правило, эти поправки определяются из измерения, охватывающие всю область измеримых расстояний. Однако такие классические процедуры вряд ли можно автоматизировать. Поэтому Leica использует другой калибровочный процесс. Как и в случае угловой калибровки, пары устройств расположены вокруг сканера таким образом, что устройства направлены друг на друга, а сканер расположен посередине. Устройства, используемые для калибровки единицы измерения расстояния, представляют собой оптоволоконные сети. Они позволяют реализовать оптические пути различной длины, требуя при этом очень небольшое пространство. Во избежание температурного воздействия на оптические волокна их размещают вне камеры окружающей среды. Для калибровки сканером выполняются измерения расстояния в двух гранях от обеих волоконных сетей. На основе этих измерений, выполненных при различных температурах, определяются зависящие от температуры калибровочные параметры и сохраняются в сканере для последующей коррекции исходных измерений.
Некоторые компоненты лазерных сканеров Z+F калибруются индивидуально, другие определяются интегрально с помощью сканирования в пределах калибровочного испытательного поля. Температурное поведение блока измерения расстояния исследуется с помощью специальной камеры. Если внутреннее опорное измерение расстояния не выполняется в сканере, то измеренные расстояния математически корректируются по обнаруженным сдвигам. Отклонения от линейности и шума определяются по калибровочной базовой линии измерения расстояния относительно интерферометра. Ссылка осуществляется с помощью трех мишеней различной отражательной способности. Обнаруженные отклонения от линейности компенсируются математически. Кроме того, значение интенсивности калибруется таким образом, чтобы получить одно и то же значение интенсивности для объекта независимо от его местоположения в области измерений расстояния.
Перед угловой калибровкой проверяется и обеспечивается механическая устойчивость сканера. Для угловой калибровки используются эталонные мишени, расположенные с высокой точностью. Расхождения между целевыми центрами, извлеченными из лазерного сканирования, и их опорные координаты используются в калибровочной модели для оценки корректирующих параметров блока отклонения. Расчетные параметры соответствуют всем уровням разрешения. Наконец, перед выдачей сертификата калибровки точность 3D-точки оценивается по отношению к целям эталонного поля [12].
Коррекция систематических ошибок в наземном лазерном сканере
Для того чтобы улучшить качество результатов измерений и приблизиться к результатам, полученным с помощью механических сенсоров при контакте, необходимо оценить погрешности, связанные с процессом измерения и исправить систематические ошибки [1]. Погрешности, связанные со сканером, могут быть либо внутренними, либо внешними. Внутренние погрешности определяются и корректируются на этапе калибровки сканера (процедура, первоначально выполняемая изготовителем). В течение нескольких лет различные исследователи интересовались определением предела оптических активных датчиков [2]. Некоторые показали, что погрешности и ошибки положения центра тяжести пятна зависит от угла раскрытия лазерного луча. Это означает, что пространственное разрешение не может быть уменьшено без увеличения шума измерения. Дифракционные пределы накладывают ограничение на разрешающую способность вдоль осей X и Y, перпендикулярных лазерному лучу, но интерференционные эффекты ограничивают разрешающую способность датчика положения вдоль оси диапазона (Z) [3]. Некоторые авторы указывают, что это так называемые «эффекты пятна» ограничивают чувствительность положения примерно до 2-5 мм. Таким образом, уменьшение погрешностей, связанных с сканером, физически ограничено. Внешние погрешности состоят, по существу, из позиционирования и ориентации датчика относительно сканируемой поверхности и, с другой стороны, других ошибок (связанных с перемещениями контрольно-измерительной машины (КИМ), природой материала сканируемой детали, шероховатостью поверхности или обработкой данных компьютером). Погрешности, связанные с системой позиционирования, определяются во время периодической калибровки КИМ. В контексте данного способа калибровки с помощью контактной пробы, лазерным сканером получают сканы, как с использованием КИМ, так и без учета этих погрешностей контрольно-измерительной машины. Ошибки, связанные с обработкой данных, а также с природой или состоянием сканируемого материала, в данной работе не рассматриваются. Данный способ калибровки НЛС сосредоточен на влиянии относительного положения (d) и углов падения (α, β) сенсора (Рис. 1) на точность измерений:
- d представляет собой расстояние вдоль средней оси лазерной плоскости, которое отделяет датчик от поверхности детали.;
- α - угол падения (в плоскости сканирования) между осью лазерной плоскости и нормальной осью измеряемой поверхности;
- β - угол ортогонального падения (в плоскости, ортогональной плоскости сканирования) между осью лазерной плоскости и нормальной осью измеряемой поверхности.
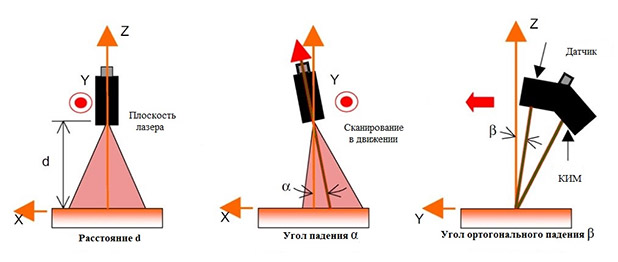
Рис. 1 Параметры позиционирования и ориентации сканера [4].
Вариации этих трех параметров оказывают большое влияние на погрешности измерений. Учет и исправление этих вызванных погрешностей можно рассматривать двумя способами: либо путем разработки теоретической модели, позволяющей учитывать их на этапе калибровки, либо путем разработки экспериментальной модели коррекции систематических погрешностей после измерения. Фаза калибровки, как правило, реализованная, позволяет определить необходимые глобальные геометрические параметры для расчета лазерной триангуляции. Обычно используемая модель является линейной и основана на модели камеры, которая состоит из одиннадцати неизвестных параметров, которые должны быть идентифицированы [4,5]. Эта модель является ограничительной и не учитывает ни сборочные дефекты оптики (которые вызывают искажения на ПЗС-датчике), ни дефекты лазерной плоскости (которые обычно представляют собой кривую). Разработка теоретической модели, позволяющей справиться с этими недостатками, довольно сложна. Тем труднее определить его параметры путем калибровки. Кроме того, модели параметрической коррекции не учитывают автоматически локальные дефекты. Поэтому для решения этой задачи был выбран подход коррекции после измерения по экспериментальной модели.
Для осуществления проектирования модели была использована экспериментальная установка, включающая влияние угла α [16]. Установка состоит из керамической пластины (калибровочного блока), а также эталонной сферы, также выполненной из керамики (см. рис. 3). Цель состоит в том, чтобы сравнить расстояние Di, измеренное лазерным сканером, с опорным расстоянием D0, измеренное контактным пробой традиционной контрольно-измерительный машиной КИМ. Измеряется расстояние Di между верхней гранью керамической пластины и центром сферы отсчета. Это означает, что всякий раз, когда изучается один из трех параметров, керамическая пластина и эталонная сфера одновременно оцифровываются.
Отсканированные облака точек, соответствующие сфере и керамической пластине, численно разделены. Метод наименьших квадратов применяется для определения связанных с ним теоретических объектов, связанных с верхней плоскостью керамической пластины и с эталонной сферой. Точка считается аберрантной, если ее расстояние до соответствующей плоскости больше, чем в два раза стандартного отклонения всех расстояний. Затем вычисляется расстояние, Di. Отклонение ei, определяемое разностью между эталонным расстоянием D0 и измеренным расстоянием Di. Затем строится корректирующая функция, которая позволяет оценить коррекцию точки, измеренной перпендикулярно измеряемой поверхности, независимо от положения измерения. Эта функция коррекции может быть использована для уменьшения систематических погрешностей измерения механических деталей:
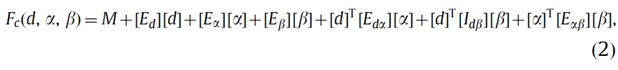
где:
- M представляет собой среднее значение всех отклонений e;
- [d], [α] и [β] представляют собой три вектора столбцов [7х1] факторов влияния;
- [Ed], [Eα] и [Eβ] представляют собой три линейных вектора [1х7] влияния каждого фактора по сравнению со средним M;
- [Ida], [Idβ] и [Iαβ] представляют собой три матрицы [7х7] эффекта взаимодействий между каждым фактором по сравнению со средним M.
Результаты разности между лазерным сканером и контактной пробой (средние значения и стандартное отклонение) представлены на рис. 2 (а) и (б) без коррекции и с глобальной и локальной коррекциями. Можно заметить, что применение локальной модели позволяет уменьшить погрешности без увеличения разброса результатов. Стандартное отклонение имеет тот же порядок величины, что и результаты, полученные без коррекции.
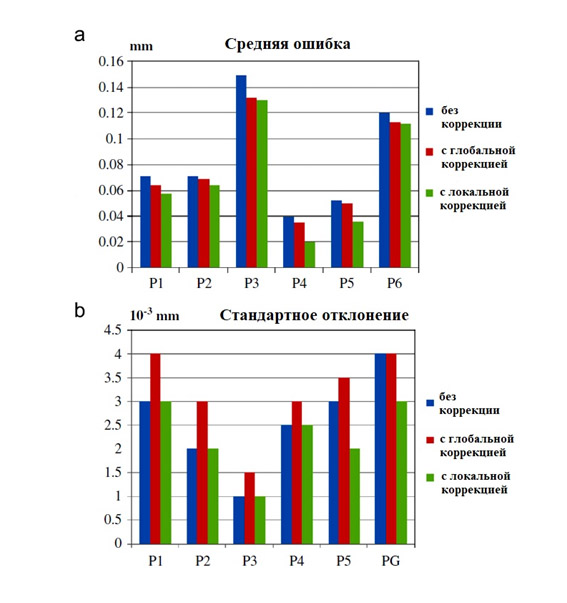
Рис. 2
(а) Сравнение средних значений разности между контактной пробой и сканирующим измерением.
(b) Сравнение стандартного отклонения разности между контактной пробой и сканирующим измерением [4].
Таким образом, в данном способе калибровки НЛС представлена экспериментальная оценка параметров, влияющих на измерения при лазерном сканировании. Исследовано влияние трех геометрических параметров позиционирования сканера относительно измеряемой детали: расстояния d, угла падения α и проекционного угла β. На основе экспериментальной оценки влияния этих трех параметров была создана модель глобальной коррекции точки измерения. Эта процедура коррекции была протестирована на усеченной пирамиде и на эталонной сфере. Поправка, примененная к измерению более или менее зависит от условий измерения. Для каждого измерения результат после коррекции всегда ближе к эталонному значению. Однако стандартное отклонение всё же было больше при применении модели коррекции. Это увеличивает погрешность, очевидно, нежелательную в метрологическом использовании. Это явление связано с изменением интенсивности света вдоль сканируемой линии. В этом смысле для улучшения метода необходимо внести дополнительную поправку в зависимости от положения измеряемой точки в поле зрения. Поправка, полученная после применения локальной модели в зависимости от параметра расстояния d, улучшает результаты. Эта модель может быть расширена до горизонтальных и вертикальных углов.
Настройка функциональной модели калибровки наземного лазерного сканера
Чтобы смягчить последствия несовершенства сканера, погрешности должны быть параметризованы, а их влияние на координаты, выводимые сканером, должно быть смоделировано детерминистически. Из-за полярного принципа измерения прибора эту модель выгодно формулировать в полярных координатах (r), а не декартовых. Одна из таких моделей:
δrij = a0 + a1rij + a2sinθij + a3sin (4πrij)/U1 + a4cos (4πrij)/U1 + a5sin (4πrij)/U2 + a6cos (4πrij)/U1 + a7sin4φij + a9cos4φij, (1)
δφij = b1 secθij + b2tanθij+b3sin2φij + b4cos2φij + b5 φij+b6cos3θij + b7sin4θij, (2)
δθij = c0 + c1θij + c2sin2θij + c3sin3φij + c4cos3φij, (3)
где rij:=[ rij,φij θij] i-я точка в пределах j-го сканирования, rij – расстояние, φij – угол вокруг вторичной оси вращения (то есть горизонтальный угол, если эта ось вертикальна), а θij – угол вокруг первичной оси вращения (то есть вертикальный угол в приведенном выше случае). Величины a0, a1, ..., c4 являются параметрами этой модели и их относят к дополнительным параметрам (ДП). Наконец, U1 и U2 – это самые короткие длины волн модуляции в случае фазового принципа измерения.
Некоторые из членов в этих уравнениях следуют непосредственно из прямого моделирования физических и геометрических свойств прибора, предполагающего аналогию с тахеометром, другие эмпирически были найдены для представления систематических отклонений, идентифицированных с помощью специальных приборов. В зависимости от используемого сканера некоторые термины могут быть опущены сразу (например, циклические отклонения расстояния).
Уравнения (1) – (3) являются достаточно общими для широкого круга практических случаев и поэтому успешно используются. Цель калибровки сканера состоит в том, чтобы оценить соответствующие значения дополнительных параметров (ДП) таким образом, чтобы систематические отклонения полярных элементов rij, производимые сканером, впоследствии могли быть смягчены (уравнение (4)):
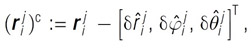
где второй вектор справа является результатом вычисления оценки (1) – (3) rij с оценочными значениями требуемых ДП. В этом контексте очень выгодно, чтобы приведенная выше модель была линейной в ДП, так как наблюдаемые полярные элементы находятся в правой части уравнений (1) – (3) и могут быть введены в качестве фиксированных параметров в регулировку без существенного изменения скорректированных значений. Это означает, что данная модель может быть использована поверх модели, реализованной производителем и уже применённой к необработанным измерениям сканера, прежде чем сделать их доступными, как rij. Во-вторых, это также означает, что наблюдаемость ДП (то есть точность, с которой они могут быть оценены) и их разделимость (то есть степень корреляции) не зависят от значения ДП и поэтому могут быть предсказаны до проведения калибровки.
Для того чтобы калибровка была полезной, скорректированные полярные элементы по состоянию на уравнение (4) должны быть более точными, чем нескорректированные полярные элементы, и смещение, вносимое в корректируемые элементы отклонениями расчетных ДП от их истинных значений, должно быть пренебрежимо малым по сравнению со стандартным отклонением полярных элементов. Это особенно важно в связи с мониторингом деформаций с использованием НЛС и ввиду потенциальной пространственной фильтрации облаков точек, которая уменьшает случайный шум, но может привести к тому, что явные смещения станут доминирующим источником ошибок. Для практических целей используется верхний предел среднеквадратического отклонения оценок ДП и верхний предел корреляции между различными параметрами подходит для оценки целесообразности ДП.
Существует несколько возможностей для проведения калибровки, в частности калибровка компонентов и калибровка системы. Первый состоит из отдельной калибровки компонентов прибора, используя специальное оборудование и процедуры, а затем составляя индивидуальные результаты. Калибровка системы НЛС означает интегральную оценку параметров по данным облака точек.
Его потенциальные преимущества включают: (I) что точное знание компонентов и их взаимодействие не требуется, (II) что она не требует специального оборудования или услуг, и (III) что она может осуществляться даже как само-калибровка и, следовательно, на рабочем месте, уступает точным и актуальным параметрам калибровки [9].
Калибровка системы НЛС может быть выполнена с использованием сигнализированных точек или геометрических объектов (например, линейность или плоскостность). Точечный подход требует, чтобы отдельные объектные точки (ОТ) идентифицировались в облаках точек. Если установленное точечное поле (многократно) используется для этой цели, ОТ может быть реализована с использованием марок, которые могут быть легко и точно расположены в облаке точек – в идеале с точностью, лучшей, чем плотность точек. Если проводится само-калибровка, то ОТ могут быть специальными марками, но они также могут быть характерными естественными точками (точечными признаками), которые могут быть обнаружены и идентифицированы при нескольких сканированиях; в этом случае ОТ будут квазислучайным образом распределены в результате характеристик сканируемой сцены. Предварительное планирование калибровки в этом случае вряд ли осуществимо. Использование геометрических объектов в отсканированной сцене вместо ОТ – это еще один вариант. Авторы провели обширное численное моделирование для случая калибровки системы на основе точечного поля со специально установленными марками в помещении, чтобы получить требования к конфигурации, помогающие планировать или оценивать, как калибровочное точечное поле, так и процесс калибровки (количество сканирований, расположение сканеров и ориентация). Они обнаружили, что даже в идеальном случае точечного поля с известными координатами объектных точек (ОТ) (например, ранее измеренными с точностью до суб-мм с помощью триангуляции) с известным местоположение сканера (например, установка на стойку) и известными углами ориентации сканера, требуется очень большое количество измерений объектных точек (порядка 37 или выше) для оценки ДП с достаточной точностью и разделяемостью, так что их смещение пренебрежимо мало по сравнению со стандартным отклонением измерений. В качестве примера на рис. 3 показана конфигурация, позволяющая оценить конкретное подмножество из 4 точек доступа (a0, b1, b2, c0) с однократным сканированием минимального количества ОТ (86 в данном случае, 26 на потолке, 2,5 м над сканером под углом возвышения 80° и 60 на полу под углом возвышения -70°). Если местоположение и ориентация сканера неизвестны, поиск конфигураций, которые дают достаточно декоррелированные ДП, особенно труден и вряд ли достижим без использования данных от датчика наклона внутри сканера в качестве прямых наблюдений наклона сканера. Численный анализ показывает, что в таких случаях может потребоваться несколько сканирований и гораздо больше 100 операций. С квазислучайным распределением ДП и неизвестным местоположением сканера, как результатом само-калибровки, мы обнаружили, что, скорее всего, вообще невозможно оценить разумные подмножества ДП с достаточной точностью и разделяемостью. Кроме того, некоторые параметры, например, масштабный коэффициент расстояния, не могут быть с пользой оценены из внутреннего точечного поля. Таким образом, наряду с анализом необходимо тщательно спланировать и создать специальное точечное поле для калибровки сканера наблюдаемости и разделимости параметров, так что калибровка на основе точечного поля может быть использована для проверки временной стабильности сканера по отношению к некоторым инструментальным несовершенствам, в то время как другие должны будут контролироваться и калиброваться на уровне компонентов. Необходимы дальнейшие исследования, чтобы дать конкретные рекомендации для такого мультимодального процесса калибровки [9].
Сложность при настройке этой полной калибровочной модели заключается, в частности, в том, что производители публикуют свои калибровочные функции и процедуры лишь в редких случаях. Для калибровки наземного лазерного сканера необходимо оценить параметры функциональной калибровочной модели в поле калибровочных точек.
Как правило, процедуры калибровки должны проводиться в условиях точности не менее чем в 3 – 10 раз лучшей, чем те, которые необходимы в данном способе. Может ли эта конвенция быть соблюдена при калибровке наземных лазерных сканеров, остается под вопросом, даже если задачи, упомянутые в этом способе, будут удовлетворительно решены [12].
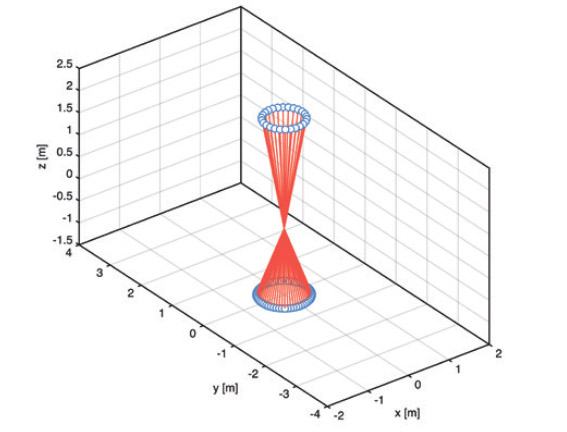
Рис 3. Минимальная конфигурация известных объектных точек (ОТ) для оценки a0, b1, b2, c0 из известной установки сканера с использованием одного сканирования в помещении высотой 4 м (сканер в положении [0, 0, 0], синие круги указывают на ОТ, красные линии указывают на соответствующую линию визирования) [11].
Способ системной калибровки панорамных лазерных сканеров с одной станции.
В данном способе представлен подход к системной калибровке панорамного наземного лазерного сканера для обеспечения высокого качества лазерного сканирования. Три основные цели этого способа заключались в следующем: а) чтобы доказать, что большинство калибровочных параметров можно оценить с одной сканирующей станции, б) доказать, что предложенная двусторонняя регулировка может дать аналогичные результаты более сложной само-калибровке, основанной на регулировке лазерного луча, и в) представить адаптацию механически интерпретируемых калибровочных параметров к системе калибровки наземных лазерных сканеров [10].
Измерения проводились в мае 2016 года в большом машинном зале, принадлежащем Боннскому университету. Насколько известно авторам, это самое большое крытое сооружение, когда-либо использовавшееся для этой цели. Размеры зала составляют примерно 71,5 × 25,0 × 8,5 м, и он был использован для того, чтобы повысить чувствительность калибровки. Большинство калибровочных параметров являются угловыми величинами и их влияние на результирующую точечную погрешность возрастает на более высоких диапазонах. Всего по всему измерительному объему было распределено 291 мишень. Целевые местоположения были обусловлены свойствами здания. Как это видно на рисунке 4, стены здания сделаны из листов поликарбоната, поддерживаемых бетонными столбами. Только задняя стена полностью сделана из бетона. Большинство мишеней были размещены на столбах, чтобы обеспечить хорошую устойчивость и хорошие отражающие свойства. Крыша здания опирается на деревянные ребра, что полезно для достижения благоприятных углов падения на более высоких высотах. [14].

Рис 4. Испытательный полигон [14]
Большинство мишеней были бумажными, основанными на официальном шаблоне Leica (Black & White) и отпечатано на плотной бумаге формата А4 (177 г/м2). Они были прикреплены клейкой лентой в заранее определенных местах на здании. Сбор данных осуществлялся в течение 24 ч после сборки опорной сети, гарантируя стабильность цели. Кроме того, 16 мишеней «Tilt & Turn», размещенные на штативах и магнитных держателях, были встроены для улучшения геометрии сети на других закрытых участках в задней части здания. Полученная конфигурация сети визуализируется на рис. 5. Большое горизонтальное рассеивание целей очевидно. Напротив, вертикальное распределение целей было ограничено. Мишени на крыше размещались выборочно из-за нехватки времени. Более того, мишени на полу использовались только в непосредственной близости от сканера, чтобы избежать углов падения более 60 градусов, как это было предложено в предыдущих исследованиях [11]. Это привело к диапазону вертикальных углов от 2 до 140 градусов и от 219 до 358 градусов (разрыв под штативом). Полученная вертикальная дисперсия мишеней обеспечивала достаточную чувствительность для хорошей оценки калибровочных параметров. Кроме того, полученные измерения расстояния варьируются от 2,2 м до 69,1 м. Важно отметить, что не каждая цель была видна с каждой станции [14].
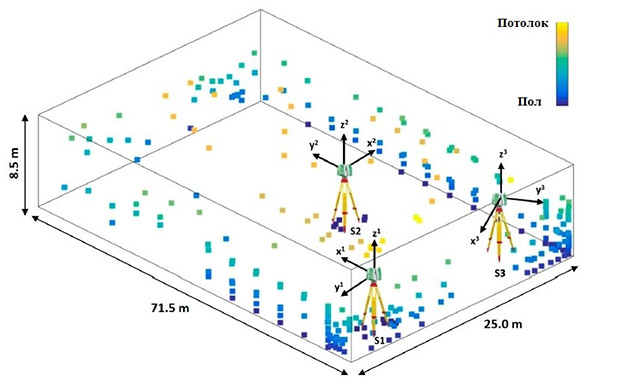
Рис 5. Конфигурация сети – расположение станций сканера (S1, S2, S3) с ориентацией локальных систем координат сканера и целевым распределением [14].
Обоснованность предложенной гипотезы была проверена в проведенных экспериментах. Новая параметризация, основанная на подлинной геометрии сканера, была адаптирована к подходу само-калибровки. В сканере были обнаружены механические рассогласования, влияющие на результаты измерений, и значения большинства калибровочных параметров были определены с заметной точностью [15].
Из этого исследования можно сделать некоторые выводы:
Большинство параметров могут быть оценены с одной сканирующей станции, без необходимости какой-либо справочной информации. Точнее, таким образом были успешно определены девять из 11 калибровочных параметров. Это означает, что время калибровки может быть значительно сокращено, в данном случае примерно с пяти до двух часов. Для того чтобы оценить все механические параметры с одной сканирующей станции, необходимы измерения. А именно, это относится к оставшимся двум параметрам, которые не чувствительны к двуликим измерениям (x10 и x5z). Предложенная двусторонняя регулировка может дать результаты, сопоставимые с обычными стратегиями само-калибровки. Несмотря на то, что он не является строгим, данный способ доказал, что является быстрым и простым решением для калибровки сканера с одной станции. Реализация новой параметризации систематической погрешности в обычном подходе само-калибровки требует некоторых модификаций. Самым интересным из них является введение калибровочного параметра x1n+2, который успешно устранил смещение от некоторых оценок параметров. Использование одного и того же набора параметров внешней ориентации для двух последовательных сканирований с одной станции сканера (двусторонние измерения) является обязательным условием калибровки сканера только с одной станции, если положение сканера не контролируется должным образом. В дальнейшем авторы планируют повторить эксперимент и использовать отдельный контроль для проверки стабильности оцениваемых параметров, что является основной мотивацией использования механических параметров.
Способ само-калибровки наземных лазерных сканеров на основе выбора наилучших геометрических параметров.
В заключительном способе представлена стратегия геометрической калибровки, используемая для повышения производительности гибридных и панорамных наземных лазерных сканеров на основе статистического анализа с помощью безразмерного индекса качества. Представленный подход использует опорную сеть точечных целей.
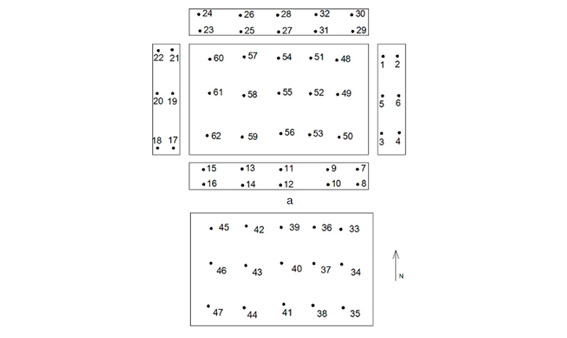
Рис 6. Опорная сеть: а) вид пола и стен, проецируемых с каждой стороны; б) вид потолка [17].
Разработка конкретной стратегии сбора данных – это необходимость максимизации наблюдаемости и восстановления дополнительных параметров. В данном способе предлагается ввести как минимум четыре станции сканирования (рис. 7); высота каждой станции сканера также должна варьироваться, и слегка наклоненное сканирование повышает точность ошибки оси коллимации по сети, включающей все номинально-уровневые сканирования для наземных лазерных сканеров [16]. Стратегия сбора данных преследует две цели: во-первых, обеспечить достаточную избыточность для корректировки; во-вторых, смягчить наличие неявных линейных корреляций между некоторыми параметрами ориентации, которые в противном случае могли бы помешать сходимость корректировки.
Конструкция опорной сети также важна, вводя корреляции в корректировку в случаях слабой геометрии. Размер калибровочной комнаты также имеет значение, играя ключевую роль для определения смещения диапазона (a0), и на самом деле требуется широкий диапазон наблюдаемых расстояний [17].
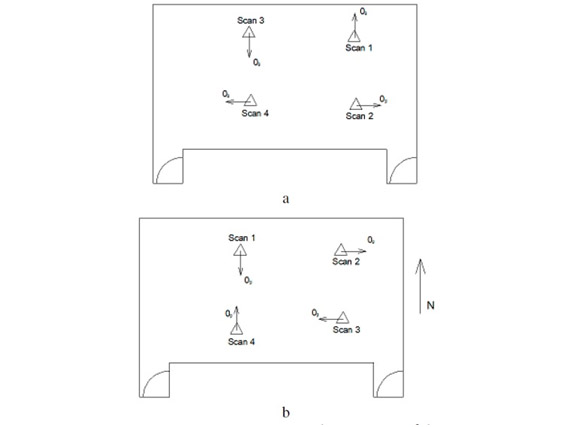
Рис 7. Станции лазерного сканера и ориентации нулевых линий внутри калибровочной комнаты: а) Leica HDS3000; б) FARO LS 880 [17].
Подход геометрической калибровки начинался с регистрации облака точек четырех сканирующих станций, достигая среднеквадратичного значения остатки на контрольных точках равны 0,002 м. Затем были исключены наблюдения с резко-отличающимися параметрами и проведено статистическое тестирование для выбора значимых дополнительных параметров с использованием стратегии. Как только резко-отличающиеся значения были обнаружены и удалены, выполняется первоначальная корректировка с полным набором параметров. В дальнейшем производится постепенное исключение дополнительных параметров. В частности, удаляются несущественные параметры, начиная с более низких значимых вероятностей, от 70%, до 99,9% [19].
Геометрическая само-калибровка может быть предпринята для обеспечения безошибочных систематических измерений. Это требует глубоких математических и статистических знаний и баланса между попытками минимизировать корреляции между параметрами и максимизировать надежность на основе статистических оценок качества. Для достижения наилучшей параметризации необходима комплексная стратегия само-калибровки. В данном способе представлены результаты калибровки двух лазерных сканеров, одного импульсного Leica HDS 3000 и фазового FARO LS 880. Улучшение точности контрольных точек первых составило в среднем почти 60% (59,3%), в то время как у второго устройства погрешности усреднялись лишь до 27% [19]. Более высокие коэффициенты улучшения были достигнуты как по среднеквадратичным ошибкам регистрации, так и по наблюдаемым с соответствующим набором дополнительных параметров. Безразмерное представленные оценки показателей качества для определения наилучшего набора дополнительных параметров настоятельно рекомендуются для успешной калибровки наземных лазерных сканеров: следует учитывать не только улучшение наблюдаемых параметров, но и улучшение параметров внешней ориентации и наземных контрольных точек. Не следует пренебрегать геометрической калибровкой наземных лазерных сканеров для улучшения выходных наборов данных, упрощая последующую обработку данных, такую как фильтрация и сглаживание. Стабильность дополнительных параметров во времени и при различных сценариях, внутренние и наружные, короткие и длинные дистанции будут дополнительно оценены в будущем. Тем не менее, большие, чем обычно, косвенные ошибки регистрации являются простыми доказательствами, которые должны встревожить пользователей об ухудшении производительности системы лазерного сканирования. Поэтому не следует недооценивать стратегию геометрической само-калибровки [20].
Список литературы
Статьи в журналах:
1. Linares JM, Bourdet P, Sprauel JM. Quality measurement on CMM integrated design and manufacturing in mechanical engineering, IDMME’2000. Kluwer Academic Publishers; 2002. 219-226.
2. Dorsch RH, Hausler G, Herrmann JM. Laser, triangulation: fundamental uncertainty in distance measurement. Applied Optics 1994:33 (7/1):1306–14.
3. Beraldin JA, Gaiani M. Evaluating the performance of close range 3D active vision systems for industrial design applications, Electronic Imaging 2005. Videometrics IX. San Jose (California, USA): NRC 47405; 2005. P. 16–20.
4. Horaud R. Vision par ordinateur. Editions Hermes, France: 1995. p. 140–54.
5. Bolles RC, Kremers JH, Cain RA. A simple sensor to gather three dimensional data. Technical Report 249, SRI International; July 1981.
6. Dantan JY, Rey R, Bourdet P. Calibrating the geometric position of a plane laser beam visio-sensor in a measuring system, In: Proceedings of the Mecatronic’s 96, Besanc-on, France; 1996. p. 233–238.
7. Cornille N, Garcia D, Sutton, S M A, Mc Neill R, Orteu JJ. Calibrage d’imageurs avec prise en compte des distorsions. Photome´canique 2004:104–25.
8. Lichti, D.; Licht, M. (2006): Experiences with terrestrial laser scanner modelling and accuracy assessment. In: Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci., 36(2006), 155 – 160.
9. Lichti, D. (2007): Error modelling, calibration and analysis of an AM-CW terrestrial laser scanner. In: ISPRS Journal of Photogrammetry and Remote Sensing, 61(2007), 307 – 324.
10. Lichti, D.; Chow, J.; Lahamya, H. (2011): Parameter de-correlation and model identification in hybrid-style terrestrial laser scanner self-calibration. In: ISPRS Journal of Photogrammetry and Remote Sensing, 66(2011), 317 – 326.
11. Walsh, G. (2016): Leica ScanStation P-Series – Details that matter. White Paper. http://leica-geosystems.com/-/media/files/products/white%20papers/leica_scanstation_p-series_details_that_matter_wp_en.ashx?la=en.
12. Tuexsen, H.-H. (2016): Werkskalibrierung und Überprüfung des Leica Scanners im Feld. In: VDVmagazin, (2016), 28 – 31.
13. Chow, J.; Ebeling, A.; Teskey, W. Low cost artificial planar target measurement techniques for terrestrial laser scanning. In Proceedings of the FIG Congress 2010: Facing the Challenges—Building the Capacity, Sydney, Australia, 11–16 April 2010.
14. García-San-Miguel, D.; Lerma, J.L. Geometric calibration of a terrestrial laser scanner with local additional parameters: An automatic strategy. ISPRS J. Photogramm. Remote Sens. 2013, 79, 122–136.
15. Gielsdorf, F.; Rietdorf, A.; Gründig, L. A Concept for the Calibration of Terrestrial Laser Scanners. In Proceedings of the FIG WorkingWeek, Athens, Greece, 22–27 May 2004.
16. Lerma, J.L.; García-San-Miguel, D. Self-calibration of terrestrial laser scanners: Selection of the best geometric additional parameters. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, 2, 219–226.
17. Glennie, C., Lichti, D.D., 2010. Static Calibration and Analysis of the Velodyne HDL-64E S2 for High Accuracy Mobile Scanning. Remote Sensing, 2(6):1610-1624.
18. Calibration of a Riegl LMS-Z429i based on a multi-station adjustment and a geometric model with additional parameters. International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences, Vol. 38, Part 3/W8, pp.177-182.
19. Reshetyuk, Y., 2009. Self-calibration and direct georeferencing in terrestrial laser scanning. Ph.D. dissertation, Royal Institute of Technology (KTH), Stockholm, Sweden, 162 p.
20. Lichti, D.D., Brüstle S., Franke, J., 2007. Self-calibration and analysis of the surphaser 25HS 3D scanner. In: Proceedings of FIG Working Week, Hong Kong SAR, China, 13-17.
студент 2-го курса магистратуры кафедры картографии и геоинформатики СПбГУ
---








 Программный комплекс ScanIMAGER предназначен для обработки результатов трехмерного лазерного сканирования применительно к архитектурным обмерам. Он построен по модульному принципу и поставляется в различных модификациях.
Программный комплекс ScanIMAGER предназначен для обработки результатов трехмерного лазерного сканирования применительно к архитектурным обмерам. Он построен по модульному принципу и поставляется в различных модификациях.