Лазерный сканер, как и любой другой измерительный прибор, нуждается в периодическом обслуживании и поверке, к тому же в процессе эксплуатации сканера его точность измерений постепенно ухудшается и, в конечном итоге, перестает удовлетворять заявленным производителем характеристикам. Таким образом, задача калибровки наземного лазерного сканера является актуальной и ее решение позволит восстановить требуемую точность измерений.
Целью данной работы явилась разработка и реализация универсального математического аппарата калибровки наземного лазерного сканера, который с учетом конструкции и принципа измерений различных сканеров мог восстановить точность измерений до величин, заявленных производителем. Методом решения задачи калибровки предлагается получение математической модели, описывающей ошибки несоответствия координат марок пространственного полигона (координаты марок которого известны с заведомо более высокой точностью, чем их можно определить по результатам сканирования) и марок, измеренных по сканам.
В статье большое внимание уделяется практической реализации технологической схемы калибровки в программных продуктах ScanIMAGER и ScanCalibr. Приводится результат тестирования метода калибровки с использованием конкретного наземного лазерного сканера, результат работы которого перестал удовлетворять заявленной производителем точности измерений.
Статья предназначена для инженерно-технических работников, применяющих технологию наземного трехмерного лазерного сканирования для решения производственных задач.
Современный наземный лазерный сканер представляет собой автоматизированную систему сбора пространственных данных, работающую с очень высокой скоростью (до 1 миллиона точек в секунду), обеспечивая при этом миллиметровую точность. В основе наземный лазерный сканер состоит из лазерного дальномера и блока развертки лазерного луча. В качестве блока развертки выступают сервопривод и полигональное зеркало или призма. Сервопривод отклоняет луч на заданную величину в горизонтальной плоскости, при этом
у большинства моделей поворачивается вся верхняя часть сканера. Развертка в вертикальной плоскости осуществляется за счет вращения или качания зеркала [1]. По принципу измерения расстояний сканеры делятся на импульсные и фазовые. Импульсный метод измерения расстояний основан на измерении времени прохождения сигнала от приемо-передающего устройства до объекта и обратно. Фазовый метод измерения основан на определении разности фаз, посылаемых и принимаемых модулированных сигналов [2]. Результатом работы лазерного сканера является растровое изображение – скан, значения пикселей которого представляют собой элементы вектора с измеренным расстоянием и интенсивностью отраженного сигнала [3]. С помощью специализированного программного обеспечения из растрового скана можно создать облако точек, пересчитав каждый пиксель скана из полярной системы координат в прямоугольную декартову с учетом результатов калибровки конкретного прибора.
В процессе эксплуатации ряд узлов лазерного сканера испытывает значительные динамические нагрузки, и со временем результаты калибровки уже не полностью компенсируют систематические ошибки прибора, что приводит к ухудшению точности выходного облака точек. Кроме того, бывают случаи, когда приходится прибегать к нестандартным условиям съемки (сканирование при значительном наклоне прибора или в перевернутом состоянии), что производителем не запрещается, но в этом случае не гарантируется точность выходного результата. При желании можно проверить точность результатов сканирования как в обычных, так и нестандартных условиях на предмет соответствия точности, заявленной производителем [4–6]. Но если точность измерений сканера перестала удовлетворять или не соответствуют заявленным требованиям, то необходимо выполнить его калибровку. Кроме того, калибровку сканера также необходимо выполнять для конкретного нестандартного случая съемки.
На сегодняшний день производители оборудования по-разному подходят к решению проблемы калибровки лазерного сканера [7–10]. Одни производители предоставляют сервисную функцию самокалибровки, но на сегодняшний день – это скорее исключение, чем правило. Вторые предлагают функцию контроля калибровки, т. е. насколько заводские калибровочные параметры актуальны и способны компенсировать ошибки сканирования, а третьи полностью отказывают в предоставлении сервисных функций, отвечающих за калибровку.
В большинстве случаев калибровка лазерного сканера – это дорогостоящая и длительная услуга, к тому же зачастую связанная с перевозом прибора через границу, поскольку в Российской Федерации отсутствуют сервисные центры большинства производителей лазерных сканеров. В то же время, как правило, задача периодической калибровки сводится к актуализации поправок, минимизирующих влияние систематических ошибок прибора на результаты сканирования, и решается на программном уровне. В данной статье рассматривается решение актуальной задачи, – разработки универсальной технологии калибровки наземных лазерных сканирующих систем по сканам испытательного полигона и специализированного программного обеспечения.
Калибровку лазерного сканера можно выполнять как по первичным данным (расстояния, горизонтальные и вертикальные углы, полученные как результат измерений в процессе сканирования), так и по вторичным данным (расстояния, горизонтальные и вертикальные углы, полученные как функции трехмерных декартовых координат, возвращаемых прибором по результатам сканирования).
Калибровка на основе первичных данных во многом является более предпочтительной, поскольку позволяет непосредственно определять и учитывать основные инструментальные ошибки сканера, вызванные неоптимальным взаимным расположением основных осей и узлов прибора (коллимационная ошибка, эксцентриситеты горизонтального и вертикального угловых отсчетных устройств и т. п.). Данные виды ошибок и методы их определения у геодезических приборов хорошо изучены, а формулы учета в результатах измерений имеют простой и законченный вид [11, 12]. Однако не всегда есть возможность выполнить калибровку сканера по первичным данным, поскольку производители оборудования часто закрывают доступ к «сырым» данным прибора и показаниям датчиков, а несанкционированная исполнителем «прошивка» внутренней памяти прибора приводит к потере гарантии. Поэтому самостоятельно калибровку сканера по первичным данным можно выполнить лишь в случае, если данная процедура предусмотрена фирмой-изготовителем как пользовательская.
В остальных же случаях единственный путь минимизировать влияние систематических ошибок и повысить качество выходной информации – это провести калибровку по расстояниям, горизонтальным и вертикальным углам, восстановленным по координатам отсканированных точек. В целях упрощения изложения данный вид калибровки далее будем называть посткалибровкой (калибровкой лазерного сканера по вторичным данным). Полученные таким образом вторичные данные отягощены не только собственно ошибками измерений, но и не вполне актуальными уже заводскими поправками. Таким образом, задача посткалибровки сводится к выявлению остаточных ошибок сканирования после
применения заводских параметров с целью их компенсации при создании выходного облака точек. Данную задачу целесообразно решать по сканам пространственного испытательного полигона, координаты марок которого известны с заведомо более высокой точностью [13], чем их можно определить по результатам сканирования.
Задачу выполнения калибровки сканера предлагается разбить на следующие этапы:
– построение пространственного испытательного полигона – печать и закрепление марок;
– построение линейно-угловой сети путем выполнения измерений на марки полигона электронным тахеометром и определение координат марок;
– сканирование полигона сканером, подлежащим калибровке, в различных положениях;
– измерение марок на сканах;
– выявление ошибок несоответствия координат марок полигона и марок, измеренных по сканам;
– вычисление полиномов компенсации ошибок;
– применение полиномов компенсации при создании облака точек.
В настоящее время приборы, которые позволяют получать круговые сканы, реализуют, как правило, одну из двух конструктивных схем. У первой из них при получении кругового скана прибор вращается в горизонтальной плоскости на 180°, а зеркало – на 360° в вертикальной плоскости. Вторая конструктивная схема предполагает полный оборот сканера в горизонтальной плоскости, и качание зеркала в вертикальной плоскости. Тем не менее, вне зависимости от схемы получения круговой развертки, в большинстве программных продуктов, она выглядит в виде растра с измерениями на 360° по горизонтальному углу и на 180° по вертикальному (рис. 1).

Рис. 1. Развертка скана 360° на 180°
Данный традиционный вид развертки для измерения углов можно использовать только для сканеров, совершающих в результате сканирования полный оборот вокруг своей оси. В случае если круговой скан получен иным способом, для определений углов развертку скана необходимо представить в соответствии с конструктивной схемой, реализованной в данном приборе. На рис. 2 показана развертка скана, полученная сканером, совершающим половину оборота вокруг своей оси и вращающим зеркало на 360°. Кроме того, в результате кругового сканирования получается зона перекрытия в несколько градусов, поэтому для корректной калибровки необходимо разделить измерения, условно говоря, на левый и правый круги или прямой и обратный ход.

Рис. 2. Измененная развертка скана 180° на 360°
В результате измерения марок испытательного полигона тахеометром и уравнивания линейно-угловой сети получается каталог точек в декартовой системе координат, который затем необходимо привести к системе координат станции сканирования ортогональным преобразованием (сдвиг и поворот по трем осям) по всем маркам по методу наименьших квадратов. Далее необходимо пересчитать координаты марок из прямоугольной декартовой системы координат в полярную (согласно принципу измерения сканера). Пересчет из прямоугольной декартовой системы координат в полярную осуществляется по следующим формулам.
Для сканера, осуществляющего при сканировании поворот по горизонтальному углу на 360°:
где H – горизонтальный угол (с учетом знаков координат для расстановки по координатным четвертям);
где V – вертикальный угол; x, y, z – координаты измерений в прямоугольной декартовой системе координат.
Для сканера, осуществляющего при сканировании поворот по горизонтальному углу на 180°:
V' = arcctg (z/√ (x2 + y2)) , (4)
где V ' – вертикальный угол для прямого хода;
где V '' – вертикальный угол для обратного хода; x, y, z – координаты марок в прямоугольной декартовой системе координат. Разделение на прямой и обратный ход осуществлялось делением каталога точек скана ровно пополам.
В качестве математической модели, описывающей ошибки несоответствия координат марок полигона и марок, измеренных по сканам, предлагается использовать представленные ниже степенные полиномы.
Для горизонтальных углов составляются уравнения вида (на примере полинома 3-й степени):
a0+a1HS+a2VS+a3HS2+a4HSVS + a5VS2 + a6HS3 + a7HS2VS + a8HsVS2 + a9VS3 = HS - HT , (6)
Для вертикальных углов составляются уравнения вида (на примере полинома 3-й степени):
b0+b1HS+b2VS+b3HS2+b4HSVS+b5VS2 + b6HS3 + b7HS2VS + b8HSVS2 + b9VS3 = VS - VT , (7)
Для дальности [14] составляются уравнения вида (на примере полинома 2-й степени):
где a0 – a9 , b0 – b9 и с0 – с9 – коэффициенты полиномов; HS – горизонтальный угол, вычисленный по координатам марки, полученным в результате сканирования; VS – вертикальный угол, вычисленный по координатам марки, полученным в результате сканирования; HT – горизонтальный угол, вычисленный по исходным координатам марки полигона, приведенным в систему станции сканирования; VT – вертикальный угол, вычисленный по исходным координатам марки полигона, приведенным в систему станции сканирования; DS – дальность до марки, вычисленная по координатам, полученным в результате сканирования; DT – дальность до марки, вычисленная по ее исходным координатам, приведенным в систему станции сканирования.
В результате решения системы уравнений по методу наименьших квадратов находим коэффициенты полиномов для горизонтального и вертикального углов, а также для дальности. На основании полученных коэффициентов полиномов можно вычислить поправку в каждое измерение, выполненное откалиброванным прибором.
Для тестирования метода калибровки был выбран скоростной фазовый лазерный сканер Faro Focus 3D S120 (рис. 3) со следующими техническими характеристиками:
– диапазон измерений: 0,6–120 м внутри/вне помещений с рассеянным светом и 90 % отражающимися поверхностями;
– скорость измерения: 122–976 тыс. точек/с;
– систематическая ошибка: ±2 мм на 10 и 25 м;
– рабочая зона по вертикали: 305°;
– рабочая зона по горизонтали: 360°;
– максимальное вертикальное разрешение: 0,009°;
– максимальное горизонтальное разрешение: 0,009°;
– максимальная скорость сканирования (вращения зеркала): 5 800 об/мин или 97 Гц.

Рис. 3. Faro Focus 3D S120
В качестве экспериментального пространственного полигона было выбрано офисное помещение. На самоклеящейся пленке были напечатаны марки типа «песочные часы» (рис. 4). Марки были наклеены равномерно по всему помещению, включая потолок и пол. Измерения марок проводились электронным тахеометром Leica TCR405 Power с учетом [13, 15]. Сканирование полигона происходило при отключенных датчиках компенсатора, барометра, GPS и компаса.
Данный лазерный сканер был выбран не случайно. В определенный момент производственного процесса, в результате сведения сканов, полученных данным сканером, в единую систему координат, было замечено, что остаточные невязки по маркам превышают допустимые значения, а также наличие двойных линий в зоне перекрытия одиночного скана, в результате чего работу прибора необходимо было подвергнуть анализу. Для этого было получено несколько сканов одного и того же полигона в различных начальных положениях сканера и несколько сканов без изменения ориентации прибора. В случае, когда начальное положение сканера изменялось, средние квадратические ошибки сведения сканов между собой составляли около 5 мм. Когда же начальное положение сканера оставалось неизменным, средние квадратические ошибки сведения сканов составляли уже менее 0,1 мм, на основании чего можно было сделать вывод, что измерения сканера стабильны и в его измерениях стабильно присутствуют систематические ошибки.
Измерение марок проводилось в программном комплексе ScanIMAGER (разработка Научно-производственного предприятия «Фотограмметрия»), в рамках которого был запрограммирован алгоритм измерения, который давал стабильное вычисление центра марки с субпиксельной точностью (рис. 5).

Рис. 4. Марка типа «Песочные часы»
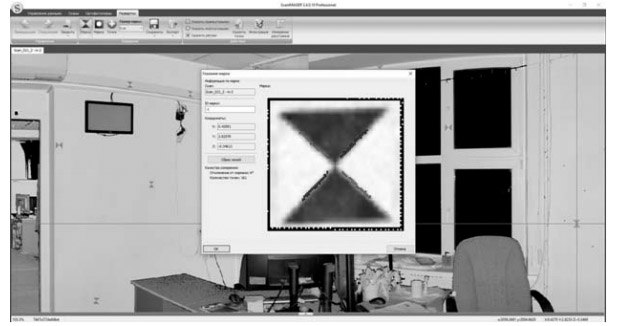
Рис. 5. Измерение марки типа «Песочные часы»
Алгоритм вычисления коэффициентов полиномов был запрограммирован в рамках программной утилиты ScanCalibr (рис. 6). Утилита позволяет добавлять несколько станций сканирования и уравнивать их совместно с целью повышения плотности покрытия результатов сканирования марками и минимизации влияния возможных грубых ошибок измерений в математической модели коррекции.
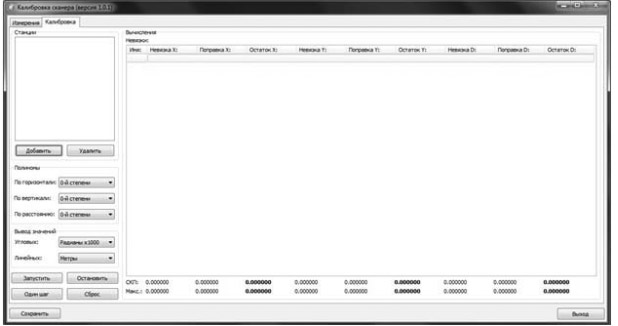
Рис. 6. Утилита калибровки сканера
Для добавления станции сканирования необходимо указать файлы измерений сканера для прямого и обратного хода, а также файл с координатами опорных марок полигона. После этого каталог опорных марок пересчитывается в систему координат каждой станции. После успешного пересчета координат выводятся параметры перехода, остаточные невязки и средние квадратические ошибки (рис. 7).
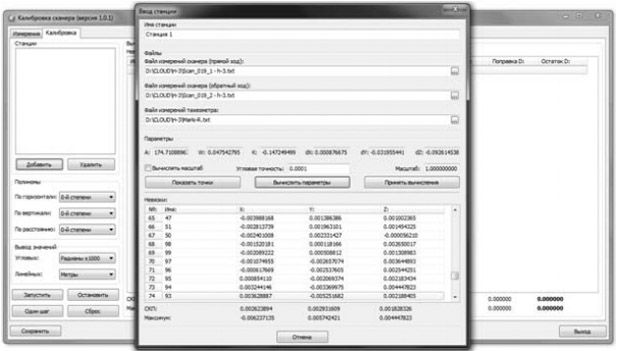
Рис. 7. Ввод новой станции
После ввода станций задаются степени полиномов для горизонтального угла, вертикального угла и дальности. Затем происходит вычисление коэффициентов полиномов с выводом невязок по каждой точке и средние квадратические отклонения (рис. 8). Изменяя степени полиномов, можно добиться минимальных остаточных невязок и сохранить результат вычислений в файл.
Алгоритм коррекции скана был запрограммирован в рамках программного продукта ScanIMAGER (разработка Научно-производственного предприятия «Фотограмметрия») в процессе конвертации скана во внутренний формат программы. В результате коррекции, невязки после регистрации сканов между собой, полученных тестируемым прибором, уменьшились в три раза. Ошибки привязки блока сканов к опорной геодезической сети, по данным тахеометрических измерений марок, уменьшились в два раза.
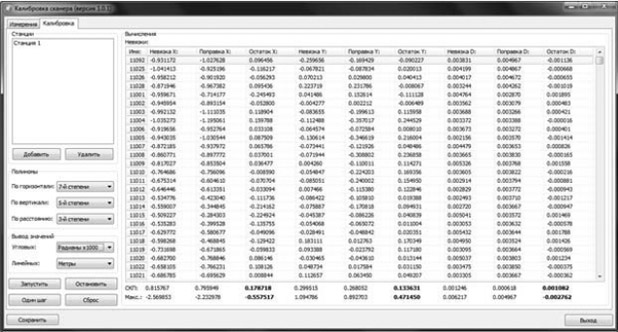
Рис. 8. Результат калибровки
На основании проведенных экспериментов и полученного результата можно сделать вывод о том, что в случае ухудшения измерительных свойств лазерного сканера и выхода их за рамки паспортных значений, посткалибровка способна восстановить точность измерений до величин, заявленных производителем. Хочется отметить, что предлагаемый метод посткалибровки ни в коей мере не призван заменить плановое обслуживание сканера у производителя, но способен в оперативном режиме и в сжатые сроки восстановить требуемую точность сканирования, а обслуживание сканера у производителя запланировать на более подходящее время. Кроме того, предлагаемый метод позволяет оперативно получить калибровочные параметры для случаев съемки с нестандартной установкой прибора, что иногда бывает полезно.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Наземное лазерное сканирование / В. А. Середович, А. В. Комиссаров, Д. В. Комиссаров, Т. А. Широкова. – Новосибирск : СГГА, 2009. – 261 с.
2. Радиогеодезические и электрооптические измерения / В. Д. Большаков, Ф. Деймлих, А. Н. Голубев, В. П. Васильев : учебник для вузов. – М. : Недра, 1985. – 303 с. ил.
3. Неволин А. Г., Медведская Т. М. Обработка результатов наземного лазерного сканирования с учетом коэффициента отражения сигнала // Вестник СГГА. – 2014. – Вып. 1 (25). – С. 47–53.
4. Чернявцев А. А., Пигин А. П. Об оперативной поверке точности сканирующих систем [Электронный ресурс] : офиц. сайт компании «Кредо-Диалог». – Режим доступа: http://www.credo-dialogue.com.
5. Широкова Т. А., Комиссаров Д. В., Комиссаров А. В. Разработка конструктивной схемы тест-объектов и методики для исследования точности наземных лазерных сканеров // ГЕО-Сибирь-2005. Науч. конгр. : сб. материалов в 7 т. (Новосибирск, 25–29 апреля 2005 г.). – Новосибирск : СГГА, 2005. Т. 5, ч. – С. 197–201.
6. Комиссаров А. В., Коркин В. С. Методика поверки наземных лазерных сканеров // Вестник СГУГиТ. – 2017. – Т. 22, № 1. – С. 110–118
7. LeicaScanStation 2. Руководство по эксплуатации. – Leica Geosystems AG, Heerbrugg, Switzerland, 2002.
8. Leica ScanStation P40/P30 User Manual. – Leica Geosystems AG, Heerbrugg, Switzerland, 2015.
9. Z+F LaserControl [Электронный ресурс] : офиц. сайт компании Zoller + Fröhlich GmbH. – Режим доступа: http://www.zf-laser.com
10. FARO Scene User Manual [Электронный ресурс]: офиц. сайт компании FARO GmbH. – Режим доступа: https://knowledge.faro.com
11. Спиридонов А. И., Кулагин Ю. Н., Кузьмин М. В. Поверка геодезических приборов. – М. : Недра, 1981. – С. 159.
12. Savveidis P. Calibrating geodetic instruments. Standard for calibration and testing // «Magazine for surveying, mapping & GIS professional» Geoinformatics. – 2004. – No. 7. – P. 18–21.
13. Никонов А. В. Исследование точности измерения расстояний электронными тахеометрами в безотражательном режиме // Вестник СГУГиТ. – 2015. – Вып. 1 (29). – С. 43–53.
14. Никонов А. В., Чешева И. Н., Лифашина Г. В. К вопросу об определении постоянной поправки дальномера электронного тахеометра // Вестник СГУГиТ. – 2015. – Вып. 1 (29) – С. 54–61.
15. Назаров И. А. Исследование влияния угла падения лазерного луча и отражающих свойств поверхности на точность измерения расстояний безотражательным электронным тахеометром [Электронный ресурс] // Интернет-вестник ВолгГАСУ. Сер.: Политематическая. – 2011. – Вып. 2 (16). – Режим доступа: http://vestnik.vgasu.ru/?source=4&articleno=548.
Получено 31.03.2019
© А. Е. Войнаровский, С. Г. Тихонов, 2019
LASER SCANNER CALIBRATION USING SCANS OF TEST POLYGON
Alexander E. Wojnarowski
Saint-Petersburg State University, 13B, Universitetskaya Emb., Saint-Petersburg, 199034, Russia, Ph. D., Associate Professor, phone: (812)992-26-85, e-mail: aw@photogrammetria.ru
Sergei G. Tikhonov
Emperor Alexander I Saint-Petersburg State Transport University, 9, Moskovsky Prospect, Saint Petersburg, 190031, Russia, Senior Lecturer, phone: (911)231-28-59, e-mail: tikhonov@photogrammetria.ru
The article deals with the implementation of the calibration technology of the ground laser scanner on the scans of the test site with the use of power polynomials. Laser scanner, like any other measuring device, needs periodic maintenance and verification, besides during the operation of the
scanner, its measurement accuracy gradually deteriorates and, ultimately, ceases to meet the manufacturer's specifications.
Thus, the problem of calibration of the ground-based laser scanner is relevant and its solution will allow to restore the required measurement accuracy.
The aim of this work was to develop and implement a universal mathematical apparatus for calibration of ground-based laser scanner, which, taking into account the design and principle of measurement of various scanners could restore the accuracy of measurements to the values stated
by the manufacturer.
The method of solving the calibration problem is proposed to obtain a mathematical model describing the errors of discrepancy between the coordinates of the marks of the spatial polygon (the coordinates of the marks of which are known with obviously higher accuracy than they can be determined by scanning results) and the marks measured by scans.
In the article great attention is paid to practical implementation of technological schemes of calibration software products ScanIMAGER and ScanCalibr. The article gives the test result of verification method of a particular ground laser scanner, the operation result of which stopped satisfying the measurement accuracy requirements specified by the producer. The article is intended for engineering and technical workers, applying ground-based 3D laser scanning technology for solving production tasks.
Key words: 3D laser scanning, scanner calibration, spatial polygon, field distortion, ScanIMAGER, ScanCalibr.
REFERENCES
1. Seredovich, V. A., Komissarov, A. V., Komissarov, D. V., & Shirokova, T. A. (2009). Nazemnoe lazernoe skanirovanie [Ground laser scaning]. Novosibirsk: SGGA Publ., 361 p. [in Russian].
2. Bol'shakov, V. D., Deymlikh, F., Golubev, A. N., & Vasil'ev, V. P. (1985). Radiogeodezicheskie i elektroopticheskie izmereniya [Radio-geodesic and electro-optical measurements]. Moscow: Nedra Publ., 303 p. [in Russian].
3. Nevolin, A. G., & Medvedskaya, T. M. (2014). Terrestrial laser scaning results processing taking into account echo signal. Vestnik SGGA [Vestnik SSGA], 1(25), 47–53 [in Russian].
4. Chernyavtsev, A. A., & Pigin, A. P. On operational verification of the accuracy of scanning systems. Official website of the company Credo Dialogue. Retrieved from http://www.credodialogue.com [in Russian].
5. Shirokova, T. A, Komissarov, A. V., & Komissarov, D. V. (2005). Development of a design scheme of test objects and methods for the study of the accuracy of ground-based laser scanners. In Sbornik materialov GEO-Sibir'-2005: T. 5, ch. ? [Proceedings of GEO-Siberia-2005: Vol.5, Part 2 (pp. 197–201). Novosibirsk: SSGA Publ. [in Russian].
6. Komissarov, A. V., & Korkin, V. S. (2017). Method of verification of terrestrial laser scanners. Vestnik SGUGiT [Vestnik SSUGT], 22(1), 110–118 [in Russian].
7. LeicaScanStation 2. (2002). User Manual. Heerbrugg: Leica Geosystems AG.
8. Leica ScanStation P40/P30. (2015). User Manual. Heerbrugg: Leica Geosystems AG.
9. Z+F LaserControl. Official website of the company Zoller + Fröhlich GmbH. Retrieved from http://www.zf-laser.com
10. FARO Scene. User Manual. Official website of the company FARO GmbH. Retrieved from https://knowledge.faro.com
11. Spiridonov, A. I., Kulagin, Yu. N., & Kuz'min, M. V. (1981). Poverka geodezicheskikh priborov [Verification of geodetic instruments] (p. 159). Moscow: Nedra Publ. [in Russian].
12. Savveidis, P. (2004). Calibrating geodetic instruments. Standard for calibration and testing. "Magazine for surveying, mapping & GIS professional" Geoinformatics, 7, 18–21.
13. Nikonov, A. V. (2015). Study of reflectionless total stations distance measurement accuracy. Vestnik SGUGiT [Vestnik SSUGT], 1(29), 43–53 [in Russian].
14. Nikonov, A. V., Chesheva, I. N., & Lifashina, G. V. (2015). Determination of total station stadia constant. Vestnik SGUGiT [Vestnik SSUGT], 1(29), 54–61 [in Russian].
15. Nazarov, I. A. (2011). A study of the influence of the angle of incidence of the laser beam and the surface reflection properties on the measurement accuracy distance reflectorless electronic total station. Internet-vestnik VolgGASU [Internet-vestnik VolgGASU], 2(16). Retrieved from http://vestnik.vgasu.ru/?source=4&articleno=548.
Received 31.03.2019
Александр Евгеньевич Войнаровский
Санкт-Петербургский государственный университет, 199034, Россия, г. Санкт-Петербург,
Университетская набережная, 7–9, кандидат технических наук, доцент, тел. (812)992-26-85,
e-mail: aw@photogrammetria.ru
Сергей Геннадьевич Тихонов
Петербургский государственный университет путей сообщения Императора Александра I,
190031, Россия, г. Санкт-Петербург, Московский пр., 9, ст. преподаватель, тел. (911)231-28-59,
e-mail: tikhonov@photogrammetria.ru
---







 Программный комплекс ScanIMAGER предназначен для обработки результатов трехмерного лазерного сканирования применительно к архитектурным обмерам. Он построен по модульному принципу и поставляется в различных модификациях.
Программный комплекс ScanIMAGER предназначен для обработки результатов трехмерного лазерного сканирования применительно к архитектурным обмерам. Он построен по модульному принципу и поставляется в различных модификациях.